Deal or No Deal is clearly America’s newest game show fetish. Hell, if it can bring Howie Mandel back from the throes of irrelevance, then it’s obviously captured the fascination of the public. Regardless, I have to add my name to the list of people who are hooked on this new TV chew toy, but I’m convinced that my love for the show is reflective of some kind of masochistic tendencies that I must be suppressing.
Let’s face it: it’s pure agony watching someone turn down hundreds of thousands of dollars in hopes that they’ll make more, only to watch them get burned in the end and settle for far less than the amount that they already turned down. Despite that, playing the risk/reward game with such large sums of money is enough to catch anybody’s attention, and I think people in general are attracted to games of this nature (Vegas, anyone?).
Last night’s show was extremely interesting because one of the contestants appeared to make the biggest bonehead move imagineable given her situation. Here was her scenario:
She had 5 suitcases left that contained the following amounts: $100, $400, $1000, $50,000, and $300,000; and the banker offered her $80,000 to quit. Deal or no deal, miss thang?
Unbelievably (to me, at least), this dumb woman, at the behest of her equally dumb husband, uttered the words the audience was just dying to hear: no deal. In a beautifully ironic fashion, the very next suitcase she opened contained $300,000, thus reinforcing the idiocy of her severely misguided decision. And of course, the audience offered up the oh-so-sympathetic and stereotypical “Ohhhhhhhhhhhhhhhhhhhhhhh.”
Don’t get me started on the studio audience…They remind me of a bunch of yahoos standing around a keg chanting “Drink! Drink! Drink!” while some socially inept reject tries to pour as much beer down his gullet as possible in order to attain five minutes of superstar status.
A closer look at the game within the game
While watching last night’s show, I had this intrinsic feeling that the woman just made a hideous decision, but at the time, I hadn’t come up with a mathematical reasoning to back my feelings. It was one of those gut instinct things that you just kind of know…ya know? This morning, however, I figured I may as well look into the math a little more just to see if I was correct in my opinion.
Oh, and I sincerely hope that one of you make it on the show someday so that you can use my “Deal or No Deal Strategy Guide” to your advantage. Anyway, on with the numbers…
If you consider only the suitcases in the scenario outlined above, then there is an 80% chance you’ll walk away with at least $30,000 less than the offer that’s currently on the table. Then again, you always have the banker in there as the x-factor, so that argument represents a worst case scenario. For me, this isn’t quite exacting enough, so now we need to look for a more defined strategy.
Enter probability theory, and more specifically, the value that you can expect to earn based on the number of remaining suitcases and their associated dollar amounts. Not surprisingly, this is astutely named – wait for it – the expected value.
At the beginning of Deal or No Deal, the contestant is presented with 26 suitcases that contain the amounts shown in the previous image, and the expected value can be calculated from the following equation:
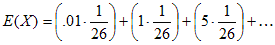
If no cases have been opened, then this value computes to approximately $131,477.54.
You mathematicians out there will already have noticed that the expected value for Deal or No Deal is simply the arithmetic mean, or more simply, the average dollar amount remaining in the cases. Risk aside, accepting a “deal” for less than the mean should generally be regarded as a gutless, weak decision, and the contestant should be ridiculed accordingly. However, late in the game, if a savvy contestant were to wrangle an amount out of the banker that is greater than the mean, then he or she ought to be carted off stage like Mike Ditka after the ’85 Super Bowl.
Okay, so maybe that’s a bit of an exaggeration, but I invite you to look at things in a purely mathematical light here. If you don’t consider “luck” to be of any help to you (and you shouldn’t – although I see you over there with that scratch-off lottery ticket!), then when you begin the game, your goal ought to be to “beat the mean.” Obviously, the mean changes as suitcases are removed, but regardless of the mean at any given time, your goal should remain the same: beat the mean.
Let’s say that you got unlucky and blew off the 13 most valuable cases on your first 13 suitcase removals. It should be abundantly clear at this point that you’re not going to walk out with a wad of cash, but you should still be expecting no less than $185.85, which is the mean. If you made it to this particular point in the game and the banker were to offer you $200, then in my less-than-humble opinion, you’d be an idiot not to take it. If you prefer facts to my freewheeling opinions, then try this on: it would be a statistical mistake not to accept this offer.
So, with this in mind, let’s revisit our woman from the scenario above. Remember her? She’s got 5 cases left that contain the following amounts: $100, $400, $1000, $50,000, and $300,000. The banker has offered her a cool $80,000 to get the hell off stage and leave in such a way as to epitomize the phrase “ignorance is bliss.”
A quick calculation reveals that the mean of the remaining amounts is $70,300. The banker’s offer is $80,000, which represents roughly a 13.8% increase over the mean. This isn’t Wall Street, but SELL SELL SELL!
Look a little closer at the reality of the situation. 80% of the remaining briefcases have at least $30,000 less than the banker’s proposed amount in them. The only guaranteed way she can do better than the proposed amount is to actually be holding the $300,000 case, because if she were to remove more cases and reveal amounts less than $300,000, the banker’s offer would likely go up to compensate for the increasing mean. Keep in mind, however, that there’s only a 20% probability of this happening! Oh, also keep in mind that the $80,000 offer is guaranteed. That’s cash money, and all bets are off! 100% chance of success…going once…going twice…Ah, forget it.
After a closer look at the numbers behind the game, it’s clear that the contestant in last night’s game made a decision that was not supported by statistical analysis. Instead of the best case scenario, which she was betting on, she actually got the worst case scenario because the next case she opened contained the $300,000. Ouch.
I haven’t mentioned it prior to now, but after that little slap in the face, the banker came back with a gaudy offer of $21,000, which was 63.1% greater than the new mean of $12,875. Looking back at this, I almost wonder if the banker had simply resorted to toying with this poor woman based on her previous decisions. Either way, the lady quickly wised up and accepted the overly generous $21,000, which represented a $110,477.54 loss against the starting mean of the game.
Statistically speaking, fewer than 25% of the contestants on the show can expect to perform worse than this lady, but then again, I guess now she doesn’t look so bad. (This comes via standard deviation analysis, which I didn’t want to bore you with)
I know it’s a game show, and I know hundreds of thousands of dollars is a lot of money, and I know how thrilling it is to go for the gusto. While statistical analysis does not really provide for “gut feeling” or “made for TV drama,” it can serve as a guide for telling you how well you can reasonably expect to do given a set of variables.
If you’ve ever been to a casino, then you know it’s never a good idea to bet solely on the best case scenario like the lady in our example. And as far as Deal or No Deal is concerned, I highly recommend that you never bet on the best “suitcase” scenario!